3.3. Definiciones: réplica, corrida, estado transitorio, estado estable, condiciones iniciales, reloj de la simulación.

Definiciones: Replica, corrida, estado transitorio,estado estable, condiciones iniciales, reloj de la simulación.

Estado estable
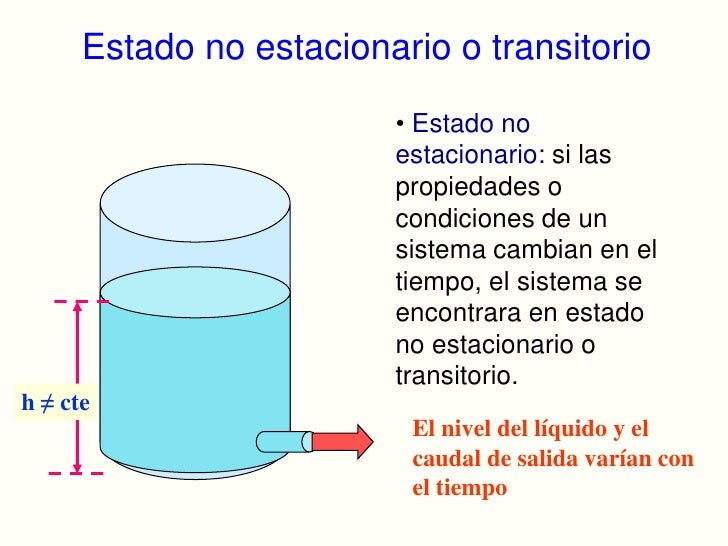
Una variable está en estado estacionario (estable) si su valores período es el mismo durante el período de tiempo que estamos considerando.Una simulación está en estado estacionario si todas sus colas lo están. El estado estacionario es alcanzado luego de un período de tiempo llamado período transitorio inicial (run-in).

Reloj de Simulación:

Es el contador de tiempo de la simulación, y su función consiste en responder preguntas tales como cuánto tiempo se ha utilizado el modelo de la simulación, y cuanto tiempo en total se requiere que dure esta última.Existen dos tipos de reloj de simulación: el reloj de simulación absoluto, quedarte del cero y termina en un tiempo total disimulación definido, el reloj de simulación relativo, que solo consiste en el lapso de tiempo que transcurre entre dos eventos. 

Ejemplo 

El tiempo de proceso de una pieza es relativo, mientras que el tiempo absoluto seria el global: desde que la pieza entro a ser procesada hasta el momento que terminó su proceso.

Estado estacionario, Condiciones y Sesgo inicial Para obtener resultados confiables:

Durante todo el tiempo en que se toman las medidas (cuando se registran los datos de la simulación) el sistema debe estar en estado estacionario. Condiciones iniciales: son los valores iniciales de los parámetros para una simulación en estado estacionario. Las condiciones iniciales determinan un sesgo inicial que influye en el tiempo que lleva alcanzar la estabilidad, en los resultados y en las estimaciones calculadas. Este sesgo se puede anular realizando simulaciones durante un período de tiempo muy largo.

Cómo obtener resultados confiables Existen 3 maneras:

1. Comenzar en estado estacionario con información del "sistema real”. Cantidad y tipo de entidades en actividad y en colas, organizadas en el calendario según información anterior y de acuerdo a sus distribuciones

2. La simulación se corre hasta alcanzar estado estacionario y se toma

“ese” estado del sistema como punto de partida para las siguientes

corridas.

3. Se corre la simulación desde el “sistema vacío” hasta el “estado estable”, allí se comienzan a recolectar datos. Se desprecian las medidas del período “run-in”.

El tercer método es el más “seguro”. En los dos primeros se corre el riesgo de

obtener datos sesgados; cuando se alcanza el estado estacionario puede variar dependiendo a veces de los distintos valores de las variables de decisión.

¿Qué es una réplica?

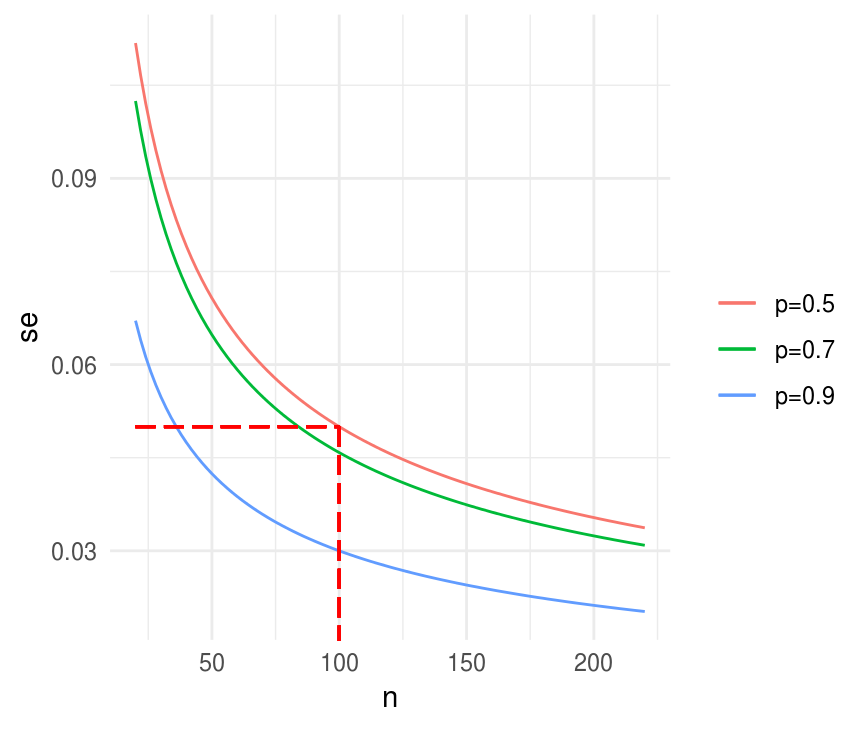
 Copia exacta o muy similar. Función de las réplicas las réplicas; se presentan con la finalidad de obtener estadísticas de intervalo que nos den una mejor ubicación del verdadero valor de la variable bajo los diferentes escenarios que se presentan al modificar los números pseudo aleatorios en cada oportunidad. Disminuir el error de la simulación Importancia de las réplicas en simulación. De esta manera se obtiene una relación entre el número de réplicas y la precisión de la estimación, de manera que entre más replicas se tengas más preciso será el modelo.

Tipos de réplicas Muestreo antitético:

es inducir una correlación negativa éntrelos elementos correspondientes en las series de números aleatorios utilizados para generar variaciones de entrada en réplicas diferentes.

Corridas comunes:

El objetivo principal es iniciar nuevas corridas de simulación utilizando siempre los datos almacenados; de esta forma, el uso de las corridas comunes afecta a todas las alternativas de igual forma. Se debe aplicar cuando el problema consiste en la comparación de dos o más alternativas.

Muestreo Clasificado:

Esta técnica se apoya en un resultado parcial de una corrida, clasificándolo como interesante o no interesante, en caso de ser interesante se continúa con la corrida en caso contrario se detiene la corrida.

Variaciones de control:

Este método utiliza aproximaciones de modelos analíticos para reducir la varianza. Muestreo estratificado: En esta técnica la función de distribución se divide en varias partes, lo más homogéneas posibles que se resuelven o ejecutan por separado; los resultados obtenidos se combinan para lograr una sola estimación del parámetro a analizar.

Muestreo sesgado:

Consiste en distorsionar las probabilidades físicas del sistema real, de tal forma que los eventos de interés ocurran más frecuentemente. Los resultados obtenidos presentarán también una distorsión que debe corregirse mediante factores probabilísticos de ajuste.

¿Cómo estimar en simulación el número de réplicas Replicas en ProModel? Para estimar el número de corridas necesarias debe realizarse un número de corridas de manera preliminar, por ejemplo, de 30 a 50. Esto se hace a través del menú de ProModel SIMULATION/OPTIONS lo que dará lugar a que se despliegue un cuadro de diálogo en el cual se agregará el número de corridas elegido en el campo "number of replications". Ahora bien, antes de emplear la fórmula para estimar el número de corridas debes elegir la variable de respuesta sobre la cual realizarás este análisis. Puede ser el contenido de alguna fila (average content), o el total de piezas producidas (current value), el tiempo en el sistema (averagedminutes in system), la utilización de máquinas o estaciones de trabajo (%utilization), etc. Todo depende del objetivo del estudio que se está realizando y enfunción de lo que se desea mejorar. A partir de que se elige la(s) variable(s) dereferencia para el análisis se recabará del reporte general ponderado la media y desviación estándar obtenida en esa variable en particular, los cuales serán

respectivamente los valores de X (la media) y σ

 (la desviación estándar) a sustituir en la siguiente fórmula: Si el número de corridas obtenido de la fórmula se cubrió con el número de corridas preliminares significa que ya no es necesario hacer más corridas; pero si el número de corridas calculado es superior al que se consideró de manera preliminar entonces deberán realizarse las corridas que sean necesarias.

PRUEBA DE CORRIDAS ARRIBA Y ABAJO

Si tenemos una secuencia de números de tal manera que a cada uno de los números siga otro mayor la secuencia dada será ascendente (arriba). Si cada número va seguido por otro menor, la secuencia será descendente (abajo)PROPIEDADES Las dos propiedades más importantes esperadas en los números aleatorios son uniformidad e independencia. La prueba de uniformidad puede ser realizada usando las pruebas de ajuste de bondad disponibles Los números pueden estar uniformemente distribuidos y aun no ser independientes uno del otro. Por ejemplo, una secuencia de números monótona mente se incrementa dentro del rango de cero a uno esta uniformemente distribuida si la cantidad_réplica, corrida, estado transitorio, estado estable, condiciones iniciales, reloj de la simulación_ incrementa es constante para todos. (0, 0.1, 0.2, 0.3, ......,0.9)

PRUEBA DE CORRIDAS

Una prueba de Corridas es un método que nos ayuda a evaluar el carácter de aleatoriedad de una secuencia de números estadística mente independientes y números uniformemente distribuidos. Es decir, dado una serie de números determinar si son o no aleatorios.

PRUEBAS DE CORRIDA ARRIBA Y ABAJO

Ahora procedemos a calcular el total de corridas que resulta de la suma de suma de corrida ascendente con la descendente.

3.2.4. Establecer el efecto que sobre la variabilidad de un estimador tiene el tamaño de la simulación

Establecer el efecto que sobre el tamaño de un estimador tiene el tamaño de la simulación.

identificar las variables cuyo comportamiento se va a simular (X)


Es decir, aquellas que se consideran que no van a tomar un valor fijo, sino que pueden tomar un rango de valores por no tratarse de variables ciertas

Concepto Monte Carlo


- Para finalizar, se lleva a cabo el análisis estadístico y de inferencia sobre el comportamiento de la realidad, siendo interesante calcular la media, la varianza y la desviación típica.


- A continuación, se sustituyen los valores simulados en el modelo matemático para ver el resultado obtenido para las simulaciones realizadas.



- Posteriormente, se agrupan y clasifican los resultados. Se comparan los casos favorables, con los casos posibles, y se agrupan por categorías de resultados.


Si no se tuvieran en cuenta dichas interrelaciones, y se simularan las variables de forma independiente, se estaría incurriendo en un error en los resultados obtenidos, y se reduciría la variabilidad de los resultados al tener lugar el efecto de compensación en la interacción de las variables.


-Una vez identificadas las variables que se van a simular, hay que determinar la función de densidad de probabilidad f(x) asociada a cada una de ellas.



- Posteriormente, se obtendrán las funciones de distribución asociadas a las variables (o variable).


Simular la realidad a través del estudio de una muestra, que se ha generado de forma totalmente aleatoria. Resulta, por tanto, de gran utilidad en los casos en los que no es posible obtener información sobre la realidad a analizar, o cuando la experimentación no es posible, o es muy costosa.


La Simulación de Monte Carlo es una técnica que permite llevar a cabo la valoración de los proyectos de inversión considerando que una, o varias, de las variables que se utilizan para la determinación de los flujos netos de caja no son variables ciertas, sino que pueden tomar varios valores.

METODOLOGÍA DE CÁLCULO

2. Estimación del tamaño de la muestra


La aplicación del método de Monte Carlo para valorar inversiones plantea dos aspectos fundamentales; la estimación de las variables y la determinación del tamaño de la muestra.


- Procedimiento aditivo: se parte de un número inicial de simulaciones (n), y se calcula la media y la desviación típica del modelo matemático utilizado.



-Se calcula la media y la desviación típica del modelo matemático utilizando para ello un número de simulaciones que asciende a "2n".


Para determinar el tamaño de la muestra, se empezará utilizando un número no demasiado elevado de simulaciones, que se sustituirán en el modelo matemático seleccionado, y se calculará la media y la desviación típica correspondiente al mismo.


Ejemplo:



Paso 1: Tamaño del bloque de simulaciones "n".



Paso 2: Tamaño del bloque de simulaciones

"n+n = 2n". Si no hay convergencia, entonces paso 3, sino finalizar.



Paso 3: Tamaño del bloque de simulaciones

"2n+n = 3n". Si no hay convergencia, entonces paso 4, sino finalizar.



Y así, sucesivamente hasta alcanzar la convergencia.


- Procedimiento multiplicativo: se parte de un número inicial de simulaciones (n), y se calcula la media y la desviación típica del modelo matemático utilizado. A continuación se procede a añadir un número de nuevas simulaciones equivalente a las acumuladas hasta ese momento, de tal forma que ahora se calcula la media y la desviación típica del modelo matemático utilizando.


INSTITUTO TECNOLÓGICO

GUSTAVO A. MADERO II


Obtenemos la variabilidad del nuevo bloque de simulaciones tiene el mismo peso sobre el total que la del bloque anterior, siendo por tanto en un método más perfecto.

1. La estimación de las variables


Ejemplo:



Paso 1: Tamaño del bloque de simulaciones "n".



Paso 2: Tamaño del bloque de simulaciones

"2xn = 2n". Si no hay convergencia, entonces paso 3, sino finalizar.



Paso 3: Tamaño del bloque de simulaciones

"2x2n = 4n". Si no hay convergencia, entonces paso 4, sino finalizar.



Y así, sucesivamente hasta alcanzar la convergencia.


SIMULACIÓN

Aplicación:

En primer lugar hay que seleccionar el modelo matemático que se va a utilizar.


Valor Actual Neto (VAN)
Tasa Interna de Rentabilidad (TIR)



Según el valor obtenido para estos métodos de valoración se tomará la decisión de si el proyecto es rentable y se lleva a cabo, o no.


3.2.4 Establecer el efecto que sobre el tamaño de un estimador tiene el tamaño de la simulación.


Z = f(x), donde "x" es la variable desconocida a simular

3.2.3. Aumentar el tamaño de la simulación y repetir

Un requerimiento lógico para un estimador es que su precisión mejore al aumentar el tamaño maestral. Es decir, que esperaremos obtener mejores estimaciones cuanto mayor sea el número de individuos.

Si se cumple dicho requerimiento, diremos que un estimador es consistente. Desde un punto de vista más riguroso diremos que un estimador es consistente si converge en probabilidad al verdadero valor del parámetro que queremos estimar.

Ejemplo:

Consideremos el caso de la estimación de la media de una población Normal (μ) y consideraremos dos estimadores:

• Estimador 1: La primera observación de la muestra (para cualquier tamaño muestra).
• Estimador 2: La media aritmética de las observaciones.

Para observar el comportamiento de ambos estimadores utilizaremos el siguiente programa que genera automáticamente diez muestras de diferentes tamaños (n = 2; 10 ; 50; 500) procedentes de una distribución Normal de parámetros  (μ = 0; σ = 1). Se tratará, por tanto, de un estudio de simulación (generamos muestras procedentes de una determinada distribución) para comparar el comportamiento de ambos estimadores. Recuerda que el verdadero valor del parámetro a estimar (μ) es cero y que corresponde a  la línea central en negro:

1) Comparad los valores del estimador 1 (primera observación) para los diferentes tamaños maestrales (n = 2; 10; 50; 500). 2) Haced lo mismo con el estimador 2: media aritmética. 3) Obtened nuevas simulaciones y repetid el estudio anterior. 4) ¿Mejora el resultado de algún estimador al aumentar el tamaño de la muestra?

Es evidente que el estimador correspondiente a la primera observación no mejora al aumentar el tamaño de la muestra. Mientras que la media aritmética converge hacia el verdadero valor del parámetro (μ = 0) al aumentar el tamaño de la muestra.

En resumen: la primera observación no es un estimador consistente de μ, mientras que la media
aritmética sí que lo es.

3.2.2. Caracterización de cada indicador: agrupamiento de datos, gráficas y estimación de parámetros

Método Secuencial Indicador

• Desarrollado por Alabert (1987b)
y Journel (1989). Es el caso correspondiente ala simulación de indicadores anidados usando el método secuencial.

• En particular si se considera un solo indicador debido a que toma valores sólo
de 0 y 1, la distribución condicional se reduce su valor esperado condicional, que en general es no conocido.

• Alabert y Journel propusieron usar en su lugar la estimación mediante kriging
simple del indicador, la cual preserva la media y la covarianza de la FA que comparado con el método de condicionamiento estándar tiene la ventaja de producir simulaciones binarias que reproducen el histograma de la FA.

• Un nuevo valor simulado se obtiene a partir de la FDP estimada usando los
valores observados (datos) y los valores previamente simulados en una vecindad del punto.

• En dependencia de cómo se estime la función distribución de probabilidad,existen dos métodos secuenciales: • Secuencial Indicador • Secuencial
Gaussiano.

• Usa el Kriging indicador para estimar la función distribución de probabilidad local.• Re
quiere del modelo del semivariograma para cada valor de corte especificado por el usuario o como alternativa más eficiente pero menos precisa del semivariograma obtenido para el valor de corte correspondiente a la mediana.

- Permite mezclar fácilmente datos duros con suaves.
- Es un algoritmo muy eficiente
- Su principal dificultad estriba en los problemas de relación de orden del Kriging de los indicadores. Como alternativa se toma en cuenta la correlación cruzada de los indicadores (co-simulación de los indicadores).

- Otro problema es que la calidad de la simulación es sensible al tamaño dela vecindad empleada por el kriging, usualmente demasiado pequeña.

3.2.1. Descripción y conceptualización de la simulación, establecer el problema, especificación del objetivo(s), definición de indicadores, simulación y determinación de la muestra.

Concepto de simulación

La palabra simulación proviene etimológica mente del latín “simulare” y su significado es imitar; aplicado en general a hechos que aparentan algo, y en realidad son otra cosa. Cuando se simula, puede hacerse aparecer algo irreal como existente, o hacer que algo que es de una manera determinada, aparezca de otro modo.

Ejemplos: “simuló ser el asesino para proteger a su padre”, “simuló un robo para cobrar el seguro”, “el profesor simuló ser un caballero medieval para que los alumnos comprendieran como se comportaban los personajes en esa época”.


El último ejemplo, muestra una técnica de enseñanza, que puede resultar muy útil, y se emplea mucho utilizando los ordenadores, pues sirven para que puedan hacerse prácticas, simulando situaciones reales, evitando exposiciones peligrosas. Por ejemplo, puede simularse entre los estudiantes de medicina la realización de una práctica quirúrgica por computadora, antes de realizar experiencias cruentas sobre seres vivos.


En el ámbito jurídico, se denomina acto simulado, cuando las partes se ponen de acuerdo para realizar una declaración de voluntad ficticia, que puede encubrir un engaño hacia un tercero; por ejemplo, simular una venta para engañar a los acreedores, llamándose en este caso simulación absoluta; o puede realizarse la simulación para esconder otro acto real, pero que se encubre con otro donde aparecen fechas, situaciones o montos diferentes, o se interponen otras personas diferentes de los verdaderos beneficiarios, llamándose en este caso la simulación, relativa. La verdadera voluntad de las partes se hace constar en un contra documento, con valor entre ellas. La simulación es lícita si no causa perjuicios a terceros.

Descripción de la Simulación

Recreación de procesos que se dan en la realidad mediante la construcción de modelos que resultan del desarrollo de ciertas aplicaciones específicas. Los programas de simulación están muy extendidos y tienen capacidades variadas, desde sencillos juegos de ordenador hasta potentes aplicaciones que permiten la experimentación industrial sin necesidad de grandes y onerosas estructuras; un caso típico de esto último seria el túnel de viento en aeronáutica.

Como proceso que es, la simulación se desarrolla a través de una serie de pasos que estructuran coherente mente el modelo y su funcionamiento en el sistema, lo desarrollan, validan, operan y analizan los resultados obtenidos.

1. Definición especialmente el problema: Como punto de partida se define la manera en que el problema establece la conexión con su entorno (interfaces).

2. Definición del modelo conceptual: Esto es explicitar los algoritmos, teorías y limites que describen al sistema, definiendo también las entradas de información requeridas y las salidas (input y output). En segundo termino, se establecen los requerimientos materiales, de personal, el tiempo que se tomara para producir y operar el modelo.

3. Recolección de los datos de entrada: Se reúne la información que será utilizada para meteorizar los datos de entrada y evaluar el rendimiento de la simulación.

4. Construcción del modelo en software: En este punto los datos obtenidos anteriormente se trasladan al lenguaje del software elegido para ejecutar las tareas de simulación. Esto aun en una fase preliminar.

5. Verificación, validez y acreditación del modelo: Se comprueba el funcionamiento correcto de simulación, considerando la recolección de los datos de entrada así como el correcto funcionamiento dentro de los parámetros establecidos.

6. Diseño experimental: Se fuerza a un estado no critico (preferentemente) la simulación para considerar nuevas militantes que partan de las diferentes fases del proceso hasta este punto.


7. Ejecución de la simulación: El momento culminante del proceso en el que se produce la información que motiva el proyecto.


8. Recolección de los datos de salida: Inicia el proceso de análisis de los resultados obtenidos de la simulación, por lo cual es necesario detallar los datos que se ha obtenido tanto del problema planteado como del proceso de simulación.

9. Análisis de datos: Interpretación de los datos en los que se definirá si el resultado es útil y por consiguiente, los aciertos y errores tanto en el planteamiento del problema como en funcionamiento de la simulación.


10. Documentación: Organización de los datos obtenidos y del análisis de estos.

11. Expansión del modelo: De acuerdo al resultado final se decide si el modelo o el sistema requieren cambios en su estructura.

objetivos de una simulación

1) Presentar una abstracción simplificada de los elementos esenciales de una situación.
2) Hacer explícitas las relaciones esenciales y las interacciones fundamentales en una situación.
3) Desarrollar la variante tiempo más rápidamente de lo normal, de manera que las implicaciones que surjan de la acción de una situación dinámica puedan ser claramente experimentadas.
4) Poner al participante en una situación de tensión, de manera que sienta el impacto directo de la toma de decisiones.
5) Ofrecer la oportunidad de participar en el proceso de enseñanza aprendizaje tomando como base las líneas de auto aprendizaje.

No hay duda que una de las ventajas más significativas de la simulación es su habilidad de acelerar el tiempo. Esta es una característica fundamental que hará posible que el participante tome decisiones sobre situaciones que normalmente se desarrollarían en un período de tiempo más largo.

En resumen, un ejercicio de simulación requiere que los participantes se conviertan en "actores de una obra", representen los papeles que son reflejo de una situación o experiencia real, y tomen las decisiones que les corresponden en su actuación.

En el caso particular de las simulaciones de hospitales que tienen que prepararse para actuar en casos de desastre, deben dar respuesta a los siguientes objetivos:


1) Familiarizar a los participantes con el proceso de toma de decisiones en circunstancias de incertidumbre y en presencia de una información confusa e inexacta.
2) Estimular a los participantes a realizar un análisis crítico de la información recibida en relación con el desastre.
3) Dar oportunidad para tomar decisiones en la mayor parte de los problemas relacionados con la emergencia creada.
4) Desarrollar el proceso de toma de decisión relativa a:


a) manejo administrativo de accidentes numerosos;
b) recursos humanos y materiales disponibles;
c) capacidad de acción frente a los desastres;
d) ampliación de capacidades hospitalarias (intra y/o extra hospitalarias);
e) preparación para casos de desastres.

5) Ayudar al participante a experimentar la tensión que resulta de tomar decisiones importantes con niveles bajos de información, o con información proveniente de fuentes no confiables.
6) Interpretar la relación que existe entre el hospital y los otros factores en una situación de desastre.
7) Fomentar el análisis de costos y de los problemas prácticos de complementación en la situación especial de falta de recursos que sigue a un estado de desastre.
8) Analizar los problemas que surgen en el manejo de voluntarios.
9) Indicar la importancia que tiene, durante un desastre, la toma de decisiones en forma coordinada y cooperativa.
10) Reconocer la necesidad de planificación y preparación previa para casos de desastre.

Definición de Indicadores


La palabra indicadores es el plural del término indicador. Un indicador es, como justamente lo dice el nombre, un elemento que se utiliza para indicar o señalar algo. Un indicador puede ser tanto concreto como abstracto, una señal, un presentimiento, una sensación o un objeto u elemento de la vida real.

Podemos encontrar indicadores en todo tipo de espacios y momentos, así como también cada ciencia tiene su tipo de indicadores que son utilizados para seguir un determinado camino de investigación.

Los indicadores pueden ser considerados como puntos de referencia, por la información e indicación que contienen pero se, pudiéndonos brindar información de tipo cuantitativa o cualitativa

La información estará formada por datos que a su vez se conforman por números, medidas, opiniones, sucesos, entre otros. Cualquiera de ellos nos permitirá conocer información sensible que nos indicará la manera de desempeñarnos a instancias de un proceso.

Los indicadores tienen como principal función señalar datos, procedimientos a seguir, fenómenos, situaciones específicas. Normalmente, cada tipo de ciencia desarrolla su propio tipo de indicadores que podrán ser más o menos efectivos y que tendrán por objetivo final guiar el análisis o estudio de los fenómenos propios de esa ciencia. En este sentido, los indicadores con los que pueden contar las ciencias empíricas, naturales y exactas pueden ser mucho más concretos, regulables y mensurables. Por el contrario, los indicadores de fenómenos, situaciones o realidades en el ámbito de las ciencias sociales están siempre mucho más cerca de ser debatidos y discutidos ya que los procesos sociales no son nunca reducibles a reglas o números.
Precisión y coherencia

Será de rigor que los indicadores contengan una extrema precisión y que se correspondan de manera coherente con el tema en análisis. También deben acomodarse a los cambios, eso los hará confiables y demostrables, y tendrán que ser sencillos de lograr.

Pensemos que se produce un suceso determinado y nos proponemos a estudiarlo, los indicadores, nos permitirán conocer de manera concreta la magnitud, la intensidad, la evolución, sus efectos y brindar un pronóstico a futuro, entre otras opciones.

Los indicadores económicos, por ejemplo, inflación, pobreza, tasa de desempleo, expresarán en números las características de la economía de una nación y a través de los números que estos reflejan podremos conocer la marcha de la misma, si la inflación es alta podremos deducir fácilmente que la economía de ese país se haya complicada.

Lo mismo ocurre con otro tipo de indicadores, como ser los demográficos, que nos permitirán conocer en números las características de una comunidad. La composición por edades, por género, su distribución, entre otras cuestiones de interés.
Aportan información sensible para desarrollar políticas

Para la gestión de gobierno, los indicadores aportan una información sensible y muy relevante ya que los mismos permiten conocer a ciencia cierta realidades del país, y en caso que corresponda, promover políticas que permitan la corrección de aquellos indicadores que se encuentran mal o por debajo de lo esperado.

Hoy, por ejemplo, es posible a través de índices como el de Desarrollo Humano (IDH) evaluar la calidad de vida de las poblaciones del mundo. Ha sido propuesto por el programa de Naciones Unidas para el desarrollo como una gran herramienta para conocer este aspecto tan importante.

Los indicadores pueden guiarnos a su vez a otro tipo de indicadores y es aquí cuando debemos hablar de indicadores jerarquizados o de diferentes niveles de indicadores ya que algunos elementos o señales más básicos pueden desembocar en indicadores más evidentes o más complejos dependiendo del caso.

Muchos aspectos de la vida cotidiana también cuentan con un número de indicadores que pueden guiarnos en nuestras actividades diarias. Por ejemplo, la casa, la ciudad, el barrio y el espacio público son todos espacios en los que encontramos miles de diferentes indicadores que determinan si podemos hacer algo o no, si nos conviene hacerlo o no, si algo es peligroso o no, si estamos yendo por el camino apropiado, si lo que pretendemos hacer dará resultado, entre otras muchas posibilidades.

Definición de Simulación

Recreación de procesos que se dan en la realidad mediante la construcción de modelos que resultan del desarrollo de ciertas aplicaciones específicas. Los programas de simulación están muy extendidos y tienen capacidades variadas, desde sencillos juegos de ordenador hasta potentes aplicaciones que permiten la experimentación industrial sin necesidad de grandes y onerosas estructuras; un caso típico de esto último seria el túnel de viento en aeronáutica.

QUÉ ES SIMULACIÓN?

La simulación computacional de sistemas, o apenas simulación, consiste en la utilización de ciertas técnicas matemáticas, empleadas en computadores, las cuales permiten imitar el funcionamiento de prácticamente cualquier tipo de operación o proceso del mundo real, es decir, es el estudio del comportamiento de sistemas reales a través del ejercicio de modelos.

Existen diversas definiciones para simulación, dentro de las cuales podemos citar la de Pegden (1990) que dice “la simulación es un proceso de proyectar un modelo computacional de un sistema real y conducir experimentos con este modelo con el propósito de entender su comportamiento y evaluar estrategias para su operación”. De esta manera, podemos entender la simulación como un proceso amplio que engloba no sólo la construcción de un modelo, sino también todo un método experimental que se sigue, buscando:
Describir el comportamiento del sistema;
Construir teorías e hipótesis considerando las observaciones efectuadas;
Usar el modelo para prever el comportamiento futuro, es decir, los efectos producidos por alteraciones en el sistema o por los métodos empleados en su operación.

Conforme descrito por Schriber (1974), en el clásico Simulation Using GPSS, para él la “simulación implica en el modelaje de un proceso o sistema, de tal forma que el modelo imite las respuestas del sistema real en una sucesión de eventos ue ocurren a lo largo del tiempo”.

Aún refiriéndonos a la simulación, podemos citar la definición de Law & amp Kelton que considera la simulación como una técnica que utiliza computadores para imitar las operaciones de varios tipos de procesos y facilidades del mundo real. También tenemos la definición de Banks que afirma “la simulación es la imitación de la operación de un proceso o sistema del mundo real a lo largo del tiempo.”

Una definición más práctica es aquella propuesta por Kelton, Sadowski &amp que dice “simulación es el proceso de proyectar y crear un modelo en un computador de un sistema real o propuesto, con el propósito de conducir experimentos numéricos para darnos una mejor comprensión del comportamiento de un dado sistema, dada una serie de condiciones.”

La lectura de estas definiciones sugiere la idea de que el modelaje y la simulación están enfocadas en la solución de problemas. Sin embargo, de acuerdo con Banks, la simulación puede también tener un nivel funcional que puede ser aplicado como:
Un dispositivo para comprensión de un problema;
Un medio de comunicación para describir la operación de un sistema;
Una herramienta de análisis para determinar elementos críticos y estimar medidas de desempeño;

Una herramienta de proyecto para evaluar problemas y proponer soluciones;
Un sistema de planeación de operaciones para trabajos, tareas y recursos;
Un mecanismo de control;
Una herramienta de entrenamiento;
Una parte del sistema para ofrecer informaciones online, proyecciones de situaciones y soporte a la decisión.

Simulación para cálculo de tamaño de muestra/poder estadístico

Cuando se esta diseñando un estudio se determina la precisión en las inferencias que se desea, y esto (junto con algunos supuestos de la población) determina el tamaño de muestra que se tomará. Usualmente se fija uno de los siguientes dos objetivos:


Se determina el error estándar de un parámetro o cantidad de interés (o de manera equivalente se fija la longitud máxima aceptable del intervalo de confianza que resultará). Por ejemplo, en encuestas electorales es típico reportar los resultados de esta encuesta más menos 33 puntos porcentuales tienen un nivel del 95%95% de confianza, ¿cúantas personas se debe entrevistar para lograr esto?


Se determina la probabilidad de que un estadístico determinado sea estadísticamente significativo. Por ejemplo, cuando se hacen ensayos clínicos se determina un tamaño de muestra para que con probabilidad de xx% se detecte una diferencia clinicamente relevante con el nuevo tratamiento (si es que este es efectivo).

En muchos casos existen fórmulas para calcular tamaños de muestra de tal manera que se cumplan los objetivos planteados, sin embargo, conforme se agrega complejidad al levantamiento de los datos (faltantes, levantamientos en varias etapas, …) o si nos alejamos de las estadísticas típicas, las fórmulas dejan de aplicar o se vuelven muy complejas, de manera que suele ser conveniente recurrir a simulación. Veremos dos ejemplos que se tomaron de Gelman and Hill (2007).

Tamaño de muestra para un error estándar determinado

Supongamos que queremos estimar el porcentaje de la población que <<<<<<< HEAD apoya la pena de muerte. Sospechamos que la proporción es 60%, imaginemos que queremos un error estándar de a lo más 0.05, o 5 puntos ======= apoya la pena de muerte. Sospechamos que la proporción es 60%60%, imaginemos que queremos una precisión (error estándar) de a lo más 0.050.05, o 55 puntos >>>>>>> 1515a1256d14479ab9c3379e463a2bb4618be6ea porcentuales. Bajo muestreo aleatorio simple, para una muestra de tamaño nn, el error estándar de la proporción pp es√p(1−p)/np(1−p)/nSustituyendo nuestra expectativa p=0.60p=0.60 llegamos a que el error estándar sería 0.49/√n0.49/n, de tal manera que si queremos se(p)≤0.05se(p)≤0.05 necesitamos n>96n>96, en el caso de proporciones es fácil determinar el tamaño de muestra de manera conservadora pues basta con suponer p=0.5p=0.5.se_fun_n <- function(n, p) sqrt(p * (1 - p) / n) xy <- data.frame(x = 20:220, y = seq(0, 1, 0.005)) ggplot(xy, aes(x = x, y = y)) + stat_function(fun = se_fun_n, args = list(p = 0.7), aes(color = "p=0.7")) + stat_function(fun = se_fun_n, args = list(p = 0.9), aes(color = "p=0.9")) + stat_function(fun = se_fun_n, args = list(p = 0.5), aes(color = "p=0.5")) + labs(x = "n", y = "se", color = "") + geom_segment(x = 20, xend = 100, y = 0.05, yend = 0.05, color = "red", alpha = 0.3, linetype = "longdash") + geom_segment(x = 100, xend = 100, y = 0.05, yend = 0, color = "red", alpha = 0.3, linetype = "longdash")




Cómo calcularíamos el tamaño de muestra simulando? En este caso es trivial calcular de manera analítica, pero nos sirve para comparar los resultados que obtendríamos con simulación.sim_p_hat <- function(n, p, n_sims = 1000){ sim_muestra <- rbinom(n_sims, size = n, prob = p) se_p_hat <- sd(sim_muestra / n) data_frame(n = n, se_p_hat = se_p_hat, p = p) } sims_.7 <- map_df(seq(20, 220, 5), ~sim_p_hat(n = ., p = 0.7)) sims_.5 <- map_df(seq(20, 220, 5), ~sim_p_hat(n = ., p = 0.5)) sims_.9 <- map_df(seq(20, 220, 5), ~sim_p_hat(n = ., p = 0.9)) sims <- bind_rows(sims_.7, sims_.5, sims_.9) ggplot(sims, aes(x = n, y = se_p_hat, color = factor(p), group = p)) + geom_smooth(se = FALSE, size = 0.5) + labs(x = "n", y = "se", color = "") + geom_segment(x = 20, xend = 100, y = 0.05, yend = 0.05, color = "red", alpha = 0.3, linetype = "longdash") + geom_segment(x = 100, xend = 100, y = 0.05, yend = 0, color = "red", alpha = 0.3, linetype = "longdash") #> `geom_smooth()` using method = 'loess' and formula 'y ~ x'

3.2. Ejemplo de una simulación tipo Monte carlo, en hoja de cálculo

https://app.box.com/s/3arziwt5ipyga6fmpar74itlkgekr81m

La simulación de MonteCarlo es una técnica que combina conceptos estadísticos (muestreo aleatorio) con la capacidad que tienen los ordenadores para generar números pseudo-aleatorios y automatizar cálculos.

Los orígenes de esta técnica están ligados al trabajo desarrollado por Stan Ulam y John Von Neumann a finales de los 40 en el laboratorio de Los Alamos, cuando investigaban el movimiento aleatorio de los neutrones [W1]. En años posteriores, la simulación de Monte Carlo se ha venido aplicando a una infinidad de ámbitos como alternativa a los modelos matemáticos exactos o incluso como único medio de estimar soluciones para problemas complejos. Así, en la actualidad es posible encontrar modelos que hacen uso de simulación Monte Carlo en las áreas informática, empresarial, económica, industrial e incluso social [5, 8]. En otras palabras, la simulación de Monte Carlo está presente en todos aquellos ámbitos en los que el comportamiento aleatorio o probabilístico desempeña un papel fundamental -precisamente, el nombre de Monte Carlo proviene de la famosa ciudad de Mónaco, donde abundan los casinos de juego y donde el azar, la probabilidad y el comportamiento aleatorio conforman todo un estilo de vida.

Son muchos los autores que han apostado por utilizar hojas de cálculo para realizar simulación Monte Carlo [1, 6, 7]. La potencia de las hojas de cálculo reside en su universalidad, en su facilidad de uso, en su capacidad para recalcular valores y, sobre todo, en las posibilidades que ofrece con respecto al análisis de escenarios (“what-if anaylisis”). Las últimas versiones de Excel incorporan, además, un lenguaje de programación propio, el Visual Basic for Applications, con el cual es posible crear auténticas aplicaciones de simulación destinadas al usuario final. En el mercado existen de hecho varios complementos de Excel (Add-Ins) específicamente diseñados para realizar simulación Monte Carlo, siendo los más conocidos: @Risk, Crystall Ball, Insight.xla, SimTools.xla, etc. [W2 – W5].



Conceptos fundamentales

La función ALEATORIO() de Excel

Las hojas de cálculo como Excel (y cualquier lenguaje de programación estándar) son capaces de generar números pseudo-aleatorios provenientes de una distribución uniforme entre el 0 y el 1. Este tipo de números pseudo-aleatorios son los elementos básicos a partir de los cuales se desarrolla cualquier simulación por ordenador. En Excel, es posible obtener un número pseudo-aleatorio -proveniente de una distribución uniforme entre el 0 y el 1- usando la función ALEATORIO:





Los números generados mediante la función ALEATORIO tienen dos propiedades que los hacen equiparables a números completamente aleatorios:


1.Cada vez que se usa la función ALEATORIO, cualquier número real entre 0 y 1 tiene la misma probabilidad de ser generado (de ahí el nombre de distribución uniforme).

2. Los diferentes números generados son estadísticamente independientes unos de otros (es decir, el valor del número generado en un momento dado no depende de los generados con anterioridad).

La función ALEATORIO es una función volátil de Excel. Esto significa que cada vez que pulsamos la tecla F9 o cambiemos alguno de los inputs del modelo, todas las celdas donde aparezca la función ALEATORIO serán recalculadas de forma automática.

Se pueden encontrar ejemplos del uso de ALEATORIO en el propio menú de ayuda de Excel.

¿Qué es la simulación de Monte Carlo?

La simulación de Monte Carlo es una técnica cuantitativa que hace uso de la estadística y los ordenadores para imitar, mediante modelos matemáticos, el comportamiento aleatorio de sistemas reales no dinámicos (por lo general, cuando se trata de sistemas cuyo estado va cambiando con el paso del tiempo, se recurre bien a la simulación de eventos discretos o bien a la simulación de sistemas continuos).

La clave de la simulación Monte Carlo consiste en crear un modelo matemático del sistema, proceso o actividad que se quiere analizar, identificando aquellas variables (inputs del modelo) cuyo comportamiento aleatorio determina el comportamiento global del sistema. Una vez identificados dichos inputs o variables aleatorias, se lleva a cabo un experimento consistente en (1) generar – con ayuda del ordenador-muestras aleatorias (valores concretos) para dichos inputs, y (2) analizar el comportamiento del sistema ante los valores generados. Tras repetir n veces este experimento, dispondremos de n observaciones sobre el comportamiento del sistema, lo cual nos será de utilidad para entender el funcionamiento del mismo –obviamente, nuestro análisis será tanto más preciso cuanto mayor sea el número n de experimentos que llevemos a cabo.

Veamos un ejemplo sencillo:

En la imagen inferior se muestra un análisis histórico de 200 días sobre el número de consultas diarias realizadas a un sistema de información empresarial (EIS) residente en un servidor central. La tabla incluye el número de consultas diarias (0 a 5) junto con las frecuencias absolutas (número de días que se producen 0, 1, ..., 5 consultas), las frecuencias relativas (10/200 = 0,05, ...), y las frecuencias relativas acumuladas.





Podemos interpretar la frecuencia relativa como la probabilidad de que ocurra el suceso asociado, en este caso, la probabilidad de un determinado número de consultas (así, p.e., la probabilidad de que se den 3 consultas en un día sería de 0,30), por lo que la tabla anterior nos proporciona la distribución de probabilidad asociada a una variable aleatoria discreta (la variable aleatoria es el número de consultas al EIS, que sólo puede tomar valores enteros entre 0 y 5).

Supongamos que queremos conocer el número esperado (o medio) de consultas por día. La respuesta a esta pregunta es fácil si recurrimos a la teoría de la probabilidad: Denotando por X a la variable aleatoria que representa el número diario de consultas al EIS, sabemos que:



Por otra parte, también podemos usar simulación de Monte Carlo para estimar el número esperado de consultas diarias (en este caso se ha podido obtener el valor exacto usando teoría de probabilidad, pero ello no siempre será factible). Veamos cómo:

Cuando se conozca la distribución de probabilidad asociada a una variable aleatoria discreta, será posible usar la columna de frecuencias relativas acumuladas para obtener los llamados intervalos de números aleatorios asociados a cada suceso.

En este caso, los intervalos obtenidos son:


• [0,00 , 0,05) para el suceso 0

• [0,05 , 0,15) para el suceso 1

• [0,15 , 0,35) para el suceso 2

• [0,35 , 0,65) para el suceso 3

• [0,65 , 0,85) para el suceso 4

• [0,85 , 1,00) para el suceso 5

El gráfico siguiente nos muestra cada una de las probabilidades sobre el número de consultas. En él, se aprecia claramente la relación existente entre probabilidad de cada suceso y el área que éste ocupa.



Esto significa que, al generar un número pseudo-aleatorio con el ordenador (proveniente de una distribución uniforme entre 0 y 1), estaremos llevando a cabo un experimento cuyo resultado, obtenido de forma aleatoria y según la distribución de probabilidad anterior, estará asociado a un suceso. Así por ejemplo, si el ordenador nos proporciona el número pseudo-aleatorio 0,2567, podremos suponer que ese día se han producido 2 consultas al EIS.

Asignamos pues la función ALEATORIO a una casilla (la G1 en el caso de la imagen):



Seleccionando la celda y “arrastrando” con el ratón desde el borde inferior derecho de la misma podemos obtener un listado completo de números pseudo-aleatorios:



A continuación, podemos usar la función SI de Excel para asignar un suceso a cada uno de los números pseudo-aleatorios generados (como veremos, otra forma de hacer esta asignación será usando la función BUSCARV):





Repitiendo el proceso de seleccionar y “arrastrar” obtendremos algo similar a:



Finalmente, usando la función PROMEDIO será posible calcular la media de los valores de la columna H:



En este caso, hemos obtenido un valor estimado que corresponde exactamente con el valor real anteriormente calculado vía la definición teórica de la media. Sin embargo, debido a la componente aleatoria intrínseca al modelo, normalmente obtendremos valores “cercanos” al valor real, siendo dichos valores diferentes unos de otros (cada simulación proporcionará sus propios resultados). Se puede comprobar este hecho pulsando repetidamente sobre la función F9 (cada vez que se pulsa dicha tecla, Excel genera nuevos valores aleatorios y, por tanto, nuevos valores para la columna H y la casilla I1). Si en lugar de usar una muestra aleatoria formada por 100 observaciones hubiésemos usado una formada por 10, los valores que obtendríamos al pulsar repetidamente F9 no serían estimaciones tan buenas al valor real. Por el contrario, es de esperar que si hubiésemos usado 1.000 (o mejor aún 10.000) observaciones, los valores que obtendríamos en la casilla I1 estarían todos muy cercanos al valor real.

Casos prácticos con software

Monte Carlo con variables discretas

Veamos un ejemplo algo más complejo del uso de Excel para construir modelos de simulación Monte Carlo cuando las variables aleatorias sean discretas:

Supongamos que trabajamos en un gran almacén informático, y que nos piden consejo para decidir sobre el número de licencias de un determinado sistema operativo que conviene adquirir – las licencias se suministrarán con los ordenadores que se vendan durante el próximo trimestre, y es lógico pensar que en pocos meses habrá un nuevo sistema operativo en el mercado de características superiores. Cada licencia de sistema operativo le cuesta al almacén un total de 75 Euros, mientras que el precio al que la vende es de 100 Euros. Cuando salga al mercado la nueva versión del sistema operativo, el almacén podrá devolver al distribuidor las licencias sobrantes, obteniendo a cambio un total del 25 Euros por cada una. Basándose en los datos históricos de los últimos meses, los responsables del almacén han sido capaces de determinar la siguiente distribución de probabilidades por lo que a las ventas de licencias del nuevo sistema operativo se refiere:



Construimos nuestro modelo usando las fórmulas que se muestran en la figura inferior. En la casilla H2 usaremos la función ALEATORIO para generar el valor pseudo-aleatorio que determinará el suceso resultante; en la celda I2 usamos la función BUSCARV para determinar el suceso correspondiente asociado al valor pseudo-aleatorio obtenido –notar que usamos también la función MIN, ya que en ningún caso podremos vender más licencias que las disponibles. El resto de fórmulas son bastante claras:



En la imagen anterior se muestra cómo construir el modelo con una observación (iteración). A fin de generar nuevas observaciones, deberemos seleccionar el rango H2:N2 y "arrastrar" hacia abajo (tantas casillas como iteraciones deseemos realizar):



Finalmente, es posible estimar el valor esperado de la variable aleatoria que proporciona los beneficios sin más que hallar la media de las 100 observaciones que acabamos de realizar. Asimismo, usaremos las funciones DESVEST e INTERVALO.CONFIANZA para hallar, respectivamente, la desviación estándar de la muestra obtenida y el intervalo de confianza (a un nivel del 95%) para el valor esperado:





A partir del modelo anterior es posible también realizar “what-if” análisis (análisis de escenarios o preguntas del tipo “¿qué pasaría si cambiamos tal o cual input?”). Para ello es suficiente con ir cambiando los valores de las celdas con fondo amarillo o rojo (inputs del modelo en este ejemplo). Asimismo, podemos ampliar fácilmente el número de iteraciones (observaciones muestrales) sin más que repetir los procesos de seleccionar y “arrastrar”.

En el caso actual, hemos optado por tomar 1.000 iteraciones para cada una de los posibles inputs asociados a la cantidad de pedido (estos posibles inputs son: 100, 150, 200, 250, y 300). Si se realizase el experimento, se obtendrían unos resultados similares a los que se muestran a continuación (ya que 1.000 es un número ya bastante considerable para este ejemplo):





A partir de los resultados, parece claro que la decisión óptima es hacer un pedido de 150 unidades, ya que con ello se consigue el beneficio máximo.

Generación de números aleatorios provenientes de otras distribuciones

Las últimas versiones de Excel incorporan un Add-In llamado Análisis de datos. Este complemento proporciona nuevas funcionalidades estadísticas a la hoja de cálculo. Entre ellas, nos interesa destacar la de Generación de números aleatorios:





Con esta opción, es posible generar fácilmente observaciones provenientes de diversas distribuciones de variable discreta (Bernoulli, Binomial, Poisson, Frecuencia relativa, y Discreta) o de variable continua (Uniforme y Normal). Independientemente del complemento Análisis de datos, es posible usar un resultado muy conocido de la teoría estadística, llamado método de la transformada inversa, para derivar las fórmulas que permiten obtener valores pseudo-aleatorios provenientes de distribuciones como la Weibull o la Lognormal. En la tabla siguiente se muestran algunas fórmulas que, implementadas en celdas de Excel, nos permiten obtener valores pseudo-aleatorios de algunas de las distribuciones continuas más usadas:





Distribución Parámetros Fórmula Excel
Exponencial Media = b = -LN(ALEATORIO())*b
Weibull Escala = b
Forma = a = b*(-LN(ALEATORIO())^(1/a)
Normal Media = μ Desv.
Estándar = σ = DISTR.NORM.INV(ALEATORIO(),μ,σ)
Lognormal Media de Ln(X) = μ
Desv. Estándar de Ln(X) = σ = DISTR.LOG.INV(ALEATORIO(),μ,σ)
Uniforme entre a y b Extremo inferior = a
Extremo superior = b = a+(b-a)*ALEATORIO()




Añadir, finalmente, que es relativamente sencillo implementar funciones VBA que, haciendo uso del método de la transformada inversa o de otros métodos similares, permitan la generación de valores provenientes de casi cualquier distribución teórica.

Simulación Monte Carlo con variables continuas

Como hemos comentado, es posible usar las fórmulas anteriores para generar, a partir de la función ALEATORIO(), valores pseudo-aleatorios provenientes de otras distribuciones continuas. En las páginas siguientes, veremos dos ejemplos de modelos que hacen uso de la distribución normal (la distribución estadística más importante y utilizada):

Ejemplo 1: Tiempo de consultas a servidores en paralelo

Supongamos que desde un ordenador cliente se realiza consultas SQL a bases de datos situadas en dos servidores distintos. Nuestro objetivo será estimar el tiempo esperado (tiempo medio) que deberemos esperar para recibir la respuesta de ambos servidores. Dada la complejidad de la consulta que queremos realizar, y basándonos en experiencias anteriores, se calcula que el tiempo necesario para que cada uno de los servidores responda a la misma sigue una distribución normal con los parámetros (media y desviación estándar, en minutos) que se indican a continuación:



Pediremos a Excel que genere valores pseudo-aleatorios provenientes de dichas distribuciones. Asimismo, usaremos la función MAX para obtener el tiempo de respuesta (que será el máximo de los tiempos de respuesta de cada servidor), y la función SI para determinar qué servidor ha sido el más rápido en responder:



Usaremos también las funciones CONTAR y CONTAR.SI para contar el número de iteraciones y el número de veces que un servidor es más rápido que el otro:



Finalmente, las funciones PROMEDIO, DESVEST, e INTERVALO.CONFIANZA nos servirán para obtener, respectivamente, el tiempo muestral medio (esperado) de respuesta, la desviación estándar de la muestra (observaciones que generaremos), y un intervalo de confianza, a un nivel del 95%, para el tiempo medio (este intervalo nos permitirá saber si nuestra estimación es buena o si, por el contrario, necesitaremos más iteraciones).

Una vez introducidas las fórmulas anteriores, bastará con seleccionar y “arrastrar” hacia abajo el rango de celdas G3:J3, con lo que se generarán nuevas iteraciones. En la imagen siguiente se muestra el resultado obtenido al generar 2.077 iteraciones. Observar que el tiempo medio estimado de respuesta es de 22,9 minutos, y podemos asegurar, con un nivel de confianza del 95%, que dicho tiempo medio estará entre 22,8 y 23,0 minutos.



Finalmente, se observa también que el servidor 1 ha respuesto más rápido que el servidor 2 en el 67% de las iteraciones.

Ejemplo 2: Inversión inicial y flujo de caja

Consideremos ahora un nuevo problema: supongamos que disponemos de un capital inicial de 250 Euros que deseamos invertir en una pequeña empresa. Supondremos también que los flujos de caja -tanto los de entrada como los de salida- son aleatorios, siguiendo éstos una distribución normal.



Para el primer mes, el valor esperado del flujo de entrada es de 500 Euros, mientras que el valor esperado para el flujo de salida es de 400 Euros. En meses posteriores, el valor esperado será el valor obtenido para en el mes anterior. Por su parte, las desviaciones estándar valdrán, en todos los casos, un 25% del valor medio (esperado) asociado. En base a lo anterior, podemos construir un modelo como se muestra en las siguientes imágenes:



Seleccionando y “arrastrando” hacia abajo el rango G3:O3, hemos obtenido los siguientes resultados para 5.859 iteraciones:



Observamos que el valor esperado para el capital final es de unos 544 Euros, y que podemos afirmar, con un nivel de confianza del 95%, que dicho valor estará entre 528 y 560 Euros.

3.1. Metodología general de la simulación

Metodología de simulación

Etapas de un proyecto de Simulación

Formulación del problema. Implica tener claros los objetivos del proyecto, y expresarlos formalmente.

Diseño del modelo conceptual. Se elabora un diseño conceptual (no ir directamente a codificar). Se puede utilizar herramientas de modelado como los diagramas de flujo o las Redes de Petri.

Recogida de datos. Se deben verificar la cantidad y calidad de los datos obtenidos. ¿Son suficientes? ¿Son confiables?

Construcción del modelo. Se construye el modelo teniendo siempre en cuenta que el propósito no es el modelo en sí, sino resolver el problema. En esta etapa se utiliza algún lenguaje de programación, lenguaje de simulación o Software especializado como GPSS, simula, simscript,Dynamo, Ithink, Powersim, Setlla, VenSim, etc (Otal, Serrano y Serrano, 2007).

Verificación y validación. La verificación implica asegurarse de que el modelo de simulación sigue las especificaciones del modelo conceptual. La validación requiere comprobar que las hipótesis de trabajo sean correctas, es decir, el modelo debe basarse en el mundo real para que sus resultados sean válidos. Para esto se puede utilizar la opinión de expertos, o bien analizar con cuánta precisión predice un dato histórico o futuro (Coss).

Análisis. Consiste en experimentar con el modelo realizado. Los autores ya mencionados hacen una interesante observación:


“el valor más importante de un estudio de simulación no son los resultados finales obtenidos con el modelo. El resultado más valioso es el conocimiento adquirido en el proceso de análisis que permite aportar argumentos cualitativos / cuantitativos justificados a favor o en contra de las diferentes opciones de diseño planteadas”.

Documentación. Es importante mantener un documento que permita saber el estado y la evolución del proyecto. El documento final servirá para informar sobre todo el proyecto. Además es útil si en algún momento alguien desea reutilizar el modelo. Se puede utilizar la siguiente estructura: Introducción, objetivos, hipótesis, descripción física del sistema, descripción del modelo, análisis de los experimentos efectuados, conclusiones.

Implementan. Consiste en tomar decisiones con base en el estudio de simulación.